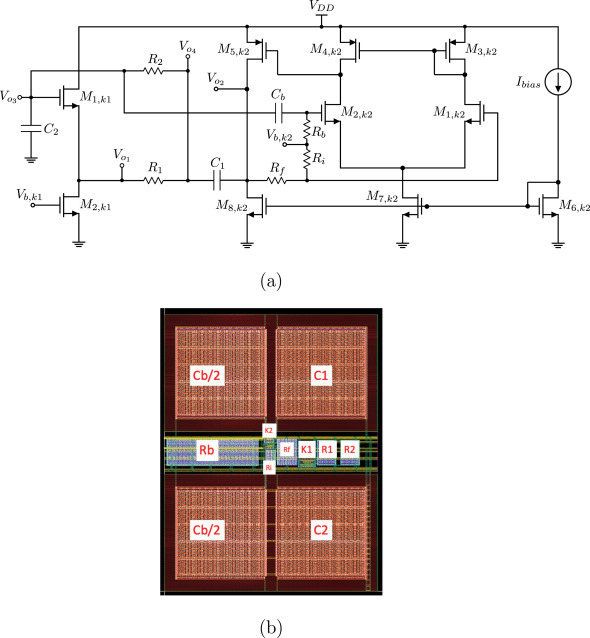
Hermite polynomials in the fractional order domain suitable for special filters design
Due to the importance of its integer order counterpart in many mathematical and engineering fields, the fractional order Hermite polynomials are studied in this paper. A fractional variation of the well known Hermite differential equation is introduced based on Caputo fractional operator. The proposed equation is solved using fractional Taylor power series method and the convergence is verified using truncated series for different values of the parameters. The condition for fractional polynomial solution is obtained and the first four polynomials are scaled using an appropriate scaling factor. The fractional order Hermite filter based on these polynomials is introduced through its magnitude response as one possible application. © 2016 IEEE.