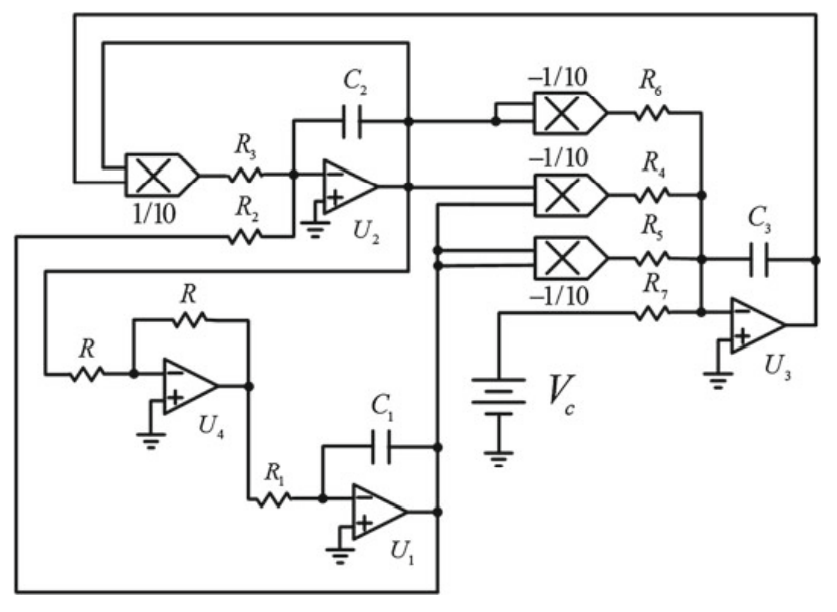
A three-dimensional no-equilibrium chaotic system: Analysis, synchronization and its fractional order form

Recently, a new classification of nonlinear dynamics has been introduced by Leonov and Kuznetsov, in which two kinds of attractors are concentrated, i.e. self-excited and hidden ones. Self-excited attractor has a basin of attraction excited from unstable equilibria. So, from that point of view, most known systems, like Lorenz's system, Rössler's system, Chen's system, or Sprott's system, belong to chaotic systems with self-excited attractors. In contrast, a few unusual systems such as those with a line equilibrium, with stable equilibria, or without equilibrium, are classified into chaotic systems with hidden attractor. Studying chaotic system with hidden attractors has become an attractive research direction because hidden attractors play an important role in theoretical problems and engineering applications. This chapter presents a three-dimensional autonomous system without any equilibrium point which can generate hidden chaotic attractor. The fundamental dynamics properties of such no-equilibrium system are discovered by using phase portraits, Lyapunov exponents, bifurcation diagram, and Kaplan-Yorke dimension. Chaos synchronization of proposed systems is achieved and confirmed by numerical simulation. In addition, an electronic circuit is implemented to evaluate the theoretical model. Finally, fractional-order form of the system with no equilibrium is also investigated. © Springer International Publishing AG 2017. All rights reserved.