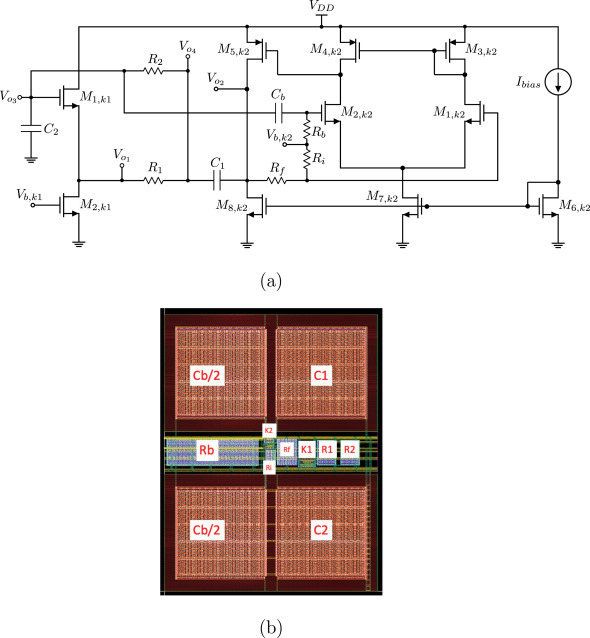
Approximation of the fractional-order laplacian Sα as a weighted sum of first-order high-pass filters
A new approximation method of the fractional-order Laplacian operator sα is introduced. The approximation is based on a weighted sum of first-order filter sections and its analytical proof is given. The optimal high-pass filter section parameters that cover six frequency decades are obtained using the flower pollination algorithm while the effect of the number of filter sections on the accuracy of the approximation is investigated. Approximations of fractional-order capacitors of orders α =0.5 and α =0.7 synthesized in Foster-II form are given as a validating example. Further, an active emulator of a fractional-order differentiator function based on this technique is also proposed and experimentally validated. © 2018 IEEE.