Breadcrumb
Implementation of a Pulsed-Wave Spectral Doppler Module on a Programmable Ultrasound System
Pulsed wave Doppler ultrasound is commonly used in the diagnosis of cardiovascular and blood flow abnormalities. Doppler techniques have gained clinical significance due to its safety, real-time performance and affordability. This work presents the development of a pulsed wave spectral Doppler module, which was integrated into a reconfigurable ultrasound system. The targeted system adopts a hardware-software partitioning scheme where an FPGA handles the front-end and a PC performs the back-end. Two factors were considered during the design. First, the data transfer rate between hardware and
Incremental Grounded Voltage Controlled Memristor Emulator
Memristor has become an interesting research subject in the recent years. Its special behavior has attracted the attention of the research community that motivated researchers to investigate it in details. As memristor is a relatively new electrical element, it is not yet available in the market as a solid state component Researchers found their way to build memristor emulators to achieve its pinched hysteresis. While many papers proposed floating emulators, only a few papers presented a grounded one. In this paper, an incremental grounded memristor emulator is proposed. The mathematical model
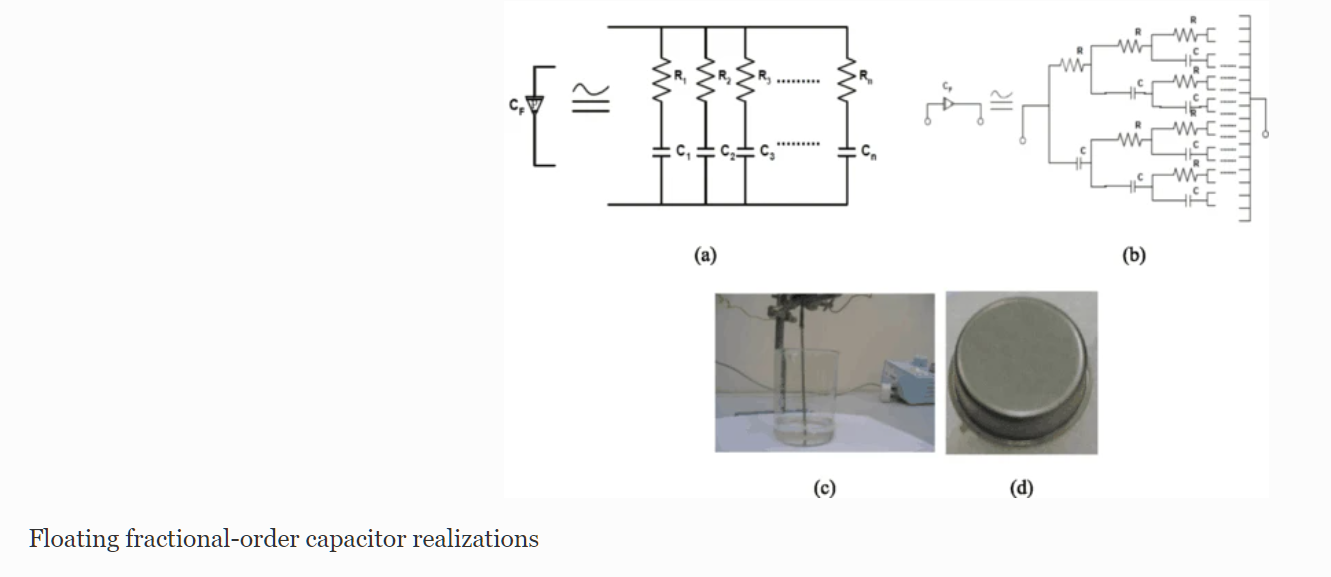
Optimization of fractional-order RLC filters
This paper introduces some generalized fundamentals for fractional-order RL β C α circuits as well as a gradient-based optimization technique in the frequency domain. One of the main advantages of the fractional-order design is that it increases the flexibility and degrees of freedom by means of the fractional parameters, which provide new fundamentals and can be used for better interpretation or best fit matching with experimental results. An analysis of the real and imaginary components, the magnitude and phase responses, and the sensitivity must be performed to obtain an optimal design
Chaotic properties of various types of hidden attractors in integer and fractional order domains
Nonlinear dynamical systems with chaotic attractors have many engineering applications such as dynamical models or pseudo-random number generators. Discovering systems with hidden attractors has recently received considerable attention because they can lead to unexpected responses to perturbations. In this chapter, several recent examples of hidden attractors, which are classified into several categories from two different viewpoints, are reviewed. From the viewpoint of the equilibrium type, they are classified into systems with no equilibria, with a line of equilibrium points, and with one
Two-dimensional front-tracking model for film evaporation
To understand the physical process involved in film evaporation, a new numerical model is created using coupled quadratic finite element formulation of the conservation equations. The heat transport equation is solved in the three different phases (solid, liquid and vapor) while the Navier-Stokes equation are solved in the two fluids. The gradient discontinuity at the liquid vapor interface provides local value of the evaporative flux density that is directly linked to the interface velocity jump through mass conservation principle and used as boundary condition for two fluid flow computations
Control design approaches for parallel robot manipulators: A review
In this article, different control design approaches for parallel robot manipulators are presented with two distinguished classes of control strategies in the literature. These are the model-free control and the dynamic control strategy, which is mainly a model-based scheme, and is mostly the alternative when the control requirements are more stringent. The authors strongly believe that this paper will be helpful for researchers and engineers in the field of robotic systems. Copyright 2017 Inderscience Enterprises Ltd.
Atmospheric pressure air microplasma current time series for true random bit generation
Generating true random bits of high quality at high data rates is usually viewed as a challenging task. To do so, physical sources of entropy with wide bandwidth are required which are able to provide truly random bits and not pseudorandom bits, as it is the case with deterministic algorithms and chaotic systems. In this work we demonstrate a reliable high-speed true random bit generator (TRBG) device based on the unpredictable electrical current time series of atmospheric pressure air microplasma (APAMP). After binarization of the sampled current time series, no further post-processing was
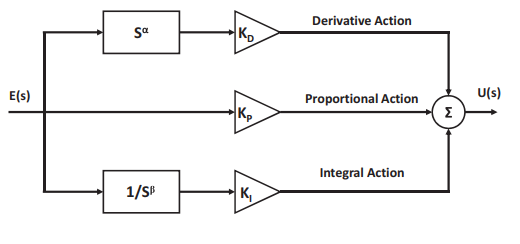
Design of fopid controller for a dc motor using approximation techniques
This paper introduces a study of fractional-order PID (FOPID) controller applied to a DC motor. The idea is to control the motor speed using the FOPID and compare it with the conventional PID controller. Two approximation techniques are employed to realize the FOPID, which are Matsuda and Oustaloup, each with order four. Different responses are depicted for various fractional orders. A specific case study for controlling the speed of a DC motor is investigated with selected fractional-orders. A comparison between the two applied techniques is proposed on the case study to determine which
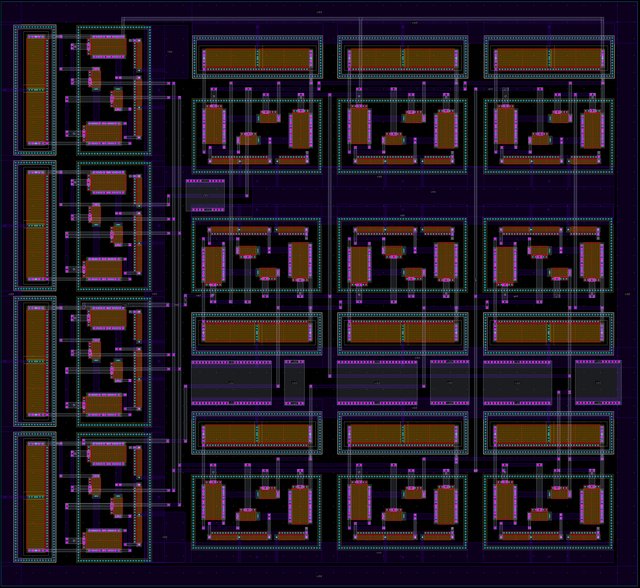
Design of low-voltage FO-[PD] controller for motion systems
Fractional-order controllers have gained significant research interest in various practical applications due to the additional degrees of freedom offered in their tuning process. The main contribution of this work is the analog implementation, for the first time in the literature, of a fractional-order controller with a transfer function that is not directly constructed from terms of the fractional-order Laplacian operator. This is achieved using Padé approximation, and the resulting integer-order transfer function is implemented using operational transconductance amplifiers as active elements
Fractional derivative modeling of double-diffusive free convection with von Neumann stability analysis
This paper focuses on the problem of fractional time derivative of fluid flow and convective heat and mass transfer from a heated semi-infinite wall immersed. We provided two cases of study, one is free convective heat transfer and the other is a free double-convective heat and mass transfer. The time-derivative terms in the equations of momentum, energy and concentration are assumed to be fractional using the Grunwald-Letnikov (GL) model. A finite difference scheme has been developed for each case of study and followed by a von Neumann stability analysis. Therefore, a stability condition has
Pagination
- Page 1
- Next page ››
