Breadcrumb

Design Of Step Pyramidal Nanoparticle For Plasmonic Photovoltaics
Plasmonic Photovoltaics (PVs) are an effective method for increasing optical absorption by adding metallic nanoparticles to the photovoltaic active layer. The role of these nanoparticles is confining the incident light near them in the PV cell, resulting in thin film PVs of enhanced efficiency. Therefore, different materials and new NPs shapes are used for this purpose. In this research, a step pyramid is introduced as a novel structure for nanoparticles for enhancing plasmonic PVs by embedding an array of the proposed step pyramid nanoparticles within the PV cell. Therefore, the extinction

Fractional order systems: An overview of mathematics, design, and applications for engineers
Fractional Order Systems: An Overview of Mathematics, Design, and Applications for Engineers introduces applications from a design perspective, helping readers plan and design their own applications. The book includes the different techniques employed to design fractional-order systems/devices comprehensively and straightforwardly. Furthermore, mathematics is available in the literature on how to solve fractional-order calculus for system applications. This book introduces the mathematics that has been employed explicitly for fractional-order systems. It will prove an excellent material for

Progressive Multi-Secret Sharing of Color Images Using Lorenz Chaotic System
Multi-Secret Image Sharing (MSIS) systems share multiple images to multiple participants in unintelligible forms that can be recovered using all the shares. This paper employs the concept of progressive secret sharing with MSIS to introduce a new system, where the number of used shares in the recovery process defines the quality of the recovered secrets. The proposed system works for any number of secret color images, and is lossless when all the shares are present. The Lorenz chaotic system, which is numerically solved using Euler method, is used as source of randomness to encrypt the secret
Accelerated Edge Detection Algorithm for High-Speed Applications
Digital Image Processing (DIP) is a growing field for various applications, such as autonomous vehicles and video surveillance. To improve the performance of DIP systems, image processing algorithms are implemented in hardware rather than software. The idea here is primarily to get a faster system than software imaging or other alternative hardware. Field-programmable gate arrays (FPGAs) have the advantages of parallel processing, low cost, and low power consumption. These semiconductor devices contain many logic blocks that can be programmed to perform everything from basic digital gate-level

Enhancement of plasmonic photovoltaics with pyramidal nanoparticles
Light trapping as a result of embedding plasmonic nanoparticles (NPs) into photovoltaics (PVs) has been recently used to achieve better optical performance compared to conventional PVs. This light trapping technique enhances the efficiency of PVs by confining incident light into hot-spot field regions around NPs, which have higher absorption, and thus more enhancement of the photocurrent. This research aims to study the impact of embedding metallic pyramidal-shaped NPs inside the PV’s active region to enhance the efficiency of plasmonic silicon PVs. The optical properties of pyramidal-shaped

Novel Fast Prediction Algorithm for Advanced and High Efficiency Video Coding
This paper introduces an efficient prediction algorithm tailored for advanced and high efficiency video coding, encompassing both H.264 and H.265. The proposed approach aims at replacing the standard intra prediction methodology by employing a streamlined prediction mode, which significantly reduces computational overhead and system complexity while eliminating the requirement for mode decision. By leveraging block comparison criteria, the designed method combines neighboring blocks in a linear fashion to accurately represent the target block. Extensive comparisons are conducted with the H.264
Small Area and Low Power Hybrid CMOS-Memristor Based FIFO for NoC
Area and power consumption are the main challenges in Network on Chip (NoC). Indeed, First Input First Output (FIFO) memory is the key element in NoC. Increasing the FIFO depth, produces an increas in the performance of NoC but at the cost of area and power consumption. This paper proposes a new hybrid CMOS-Memristor based FIFO architecture that consumes low power and has a small size compared to the conventional CMOS-based FIFOs. The predicted area is approximately equal to the half of that wasted in conventional FIFOs. The implementation of FIFO controller module is implemented using HDL
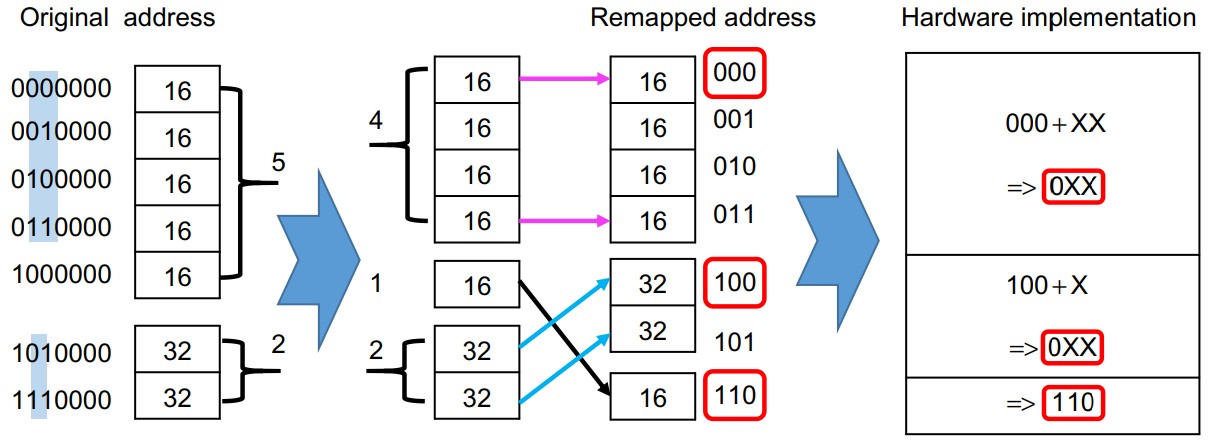
FPGA Implementation of Fractional-Order Chaotic Systems
This chapter introduces two FPGA implementations of the fractional-order operators: the Caputo and the Grünwald-Letnikov (GL) derivatives. First, the Caputo derivative is realized using nonuniform segmentation to reduce the size of the Look-Up Table. The Caputo implementation introduced can generate derivatives of previously defined functions only. Generic and complete hardware architecture of the GL operator is realized with different memory window sizes. The generic architecture is used as a block to implement several fractional-order chaotic systems. The investigated systems include Borah
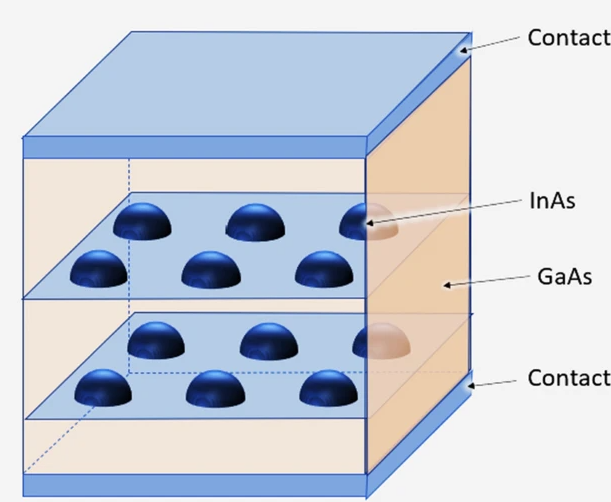
Modeling of dark current in semispherical quantum dot structures for infrared photodetection
Due to its tunable heterojunction bandgap and great sensitivity to normal incident illumination, the Quantum Dot Infrared Photodetectors (QDIPs) have received a lot of attention for the purpose of infrared sensing. It could be a very promising replacement for conventional infrared photodetectors made with established technology, including mercury cadmium telluride and quantum well infrared photodetectors. In this work, a model for the dark current in semispherical QDIP has been developed, resolves the primary semiconductor Poisson's and continuity equations, where the wave function and the

Mathematical Techniques of Fractional Order Systems
Mathematical Techniques of Fractional Order Systems illustrates advances in linear and nonlinear fractional-order systems relating to many interdisciplinary applications, including biomedical, control, circuits, electromagnetics and security. The book covers the mathematical background and literature survey of fractional-order calculus and generalized fractional-order circuit theorems from different perspectives in design, analysis and realizations, nonlinear fractional-order circuits and systems, the fractional-order memristive circuits and systems in design, analysis, emulators, simulation
Pagination
- Previous page ‹‹
- Page 4
- Next page ››
